1.2 Exercises
Work through examples 1.2.1 through 1.2.5 again using variables as follows:
Step 1: Write an equation for each scale using the variables below
t = the weight of one triangle
c = the weight of one circle
s = the weight of one star
q = the weight of one square
For example, if the (balanced) scale has 4 triangles on one side, and a circle, and a square on the other side, then we write 4t = c + q as the equation.
Step 2: Manipulate these equations to answer the questions. Some manipulations include adding/subtracting equations to get a new equation that is more useful and/or solving for a variable in one equation and plugging it into another equation. Try to avoid using fractions. Show and explain every step. That is, justify where each new equation comes from.
Step 3: State your final answer as a complete sentence (for example: 3 triangles will balance the last scale)
Example 1.2.1 Revisited
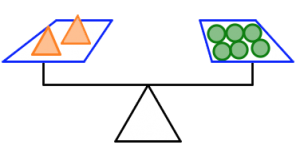
a) Based on the scale picture, what can you say about the relationship between the weight of a star and the weight of a circle? Explain how you determined your answer.
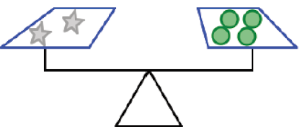
b) Based on the scale picture what can you say about the relationship between the weight of a star and the weight of a square? Explain how you determined your answer.
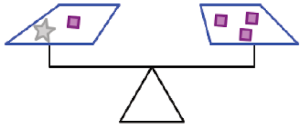
Example 1.2.2 Revisited
Use Figure 1 to answer the questions that follow.
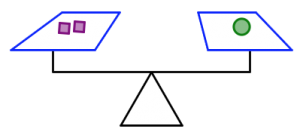
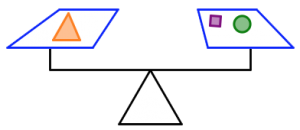
a) Which shape weighs the most? Justify your answer.
b) Which scale is holding the most total weight? How do you know?
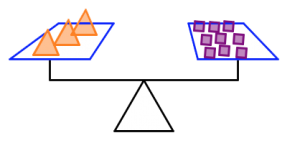
Example 1.2.3 Revisited
Use the first two scale pictures in the Figure 2 to gather enough information to determine how many squares go in place of the question mark in the third scale picture.

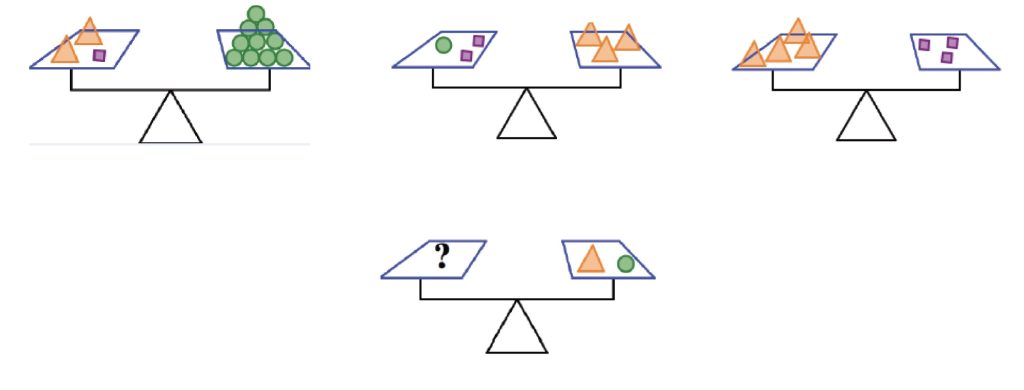
Example 1.2.4 Revisited
Use the first three scale pictures in Figure 3 to gather information to determine what shapes will balance the scale below. That is, what can we put in place of the question mark that will balance the scale? Try to come up with more than one answer. Explain how you arrived at your answers.
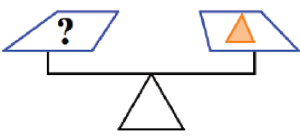
Example 1.2.5 Revisited
Use the scale pictures in Figure 4 to gather information to determine how many squares go in place of each of the question marks in parts (a), (b) and (c) below.

a)
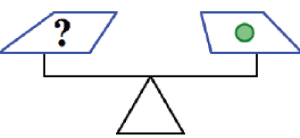
b)
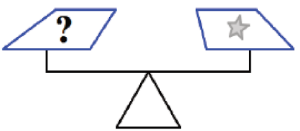
c)
a letter that represents a quantity that may vary
a statement (with an equal sign) asserting that two expressions have the same numerical value

