4.1 Exercises
From CourseHero https://www.coursehero.com/file/85655103/Linear-Functions-HWdoc/
Slope-Intercept Form: [latex]y=mx+b[/latex]
Determine the slope and y-intercept for each graph. Write the equation for the graph in slope-intercept form.
1.
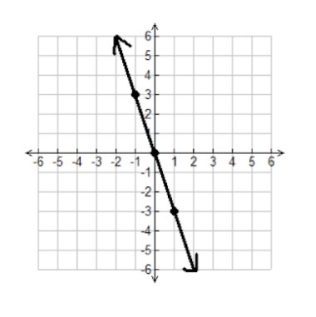
Slope:
y-intercept:
Equation:
2.
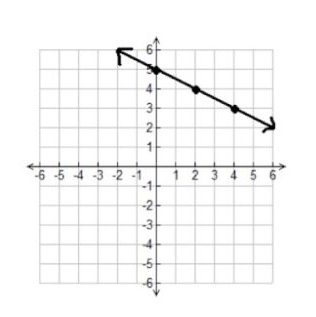
Slope:
y-intercept:
Equation:
3.
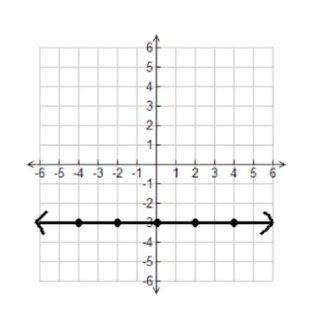
Slope:
y-intercept:
Equation:
Write each equation in slope-intercept form, identify the slope and y-intercept, then graph each equation. Clearly mark at least three points on each line. Show your work. Label the x- and y-axis.
4. [latex]y=6[/latex]
Slope:
y-intercept:
5. [latex]x-y=4[/latex]
Slope:
y-intercept:

6. [latex]5x-3y=24[/latex]
Slope:
y-intercept:

7. [latex]2x+y=0[/latex]
Slope:
y-intercept:

8. [latex]-x+4y=4[/latex]
Slope:
y-intercept:

9. [latex]x=-4[/latex]
Slope:
y-intercept:

Determine the slope (rate of change) and the y-intercept (start value) for each table. Write an equation in slope-intercept form.
10.
| x | y |
| -2 | 0 |
| 0 | 10 |
| 25 | 20 |
| 4 | 30 |
| 6 | 40 |
Slope:
y-intercept:
Equation:
11.
| x | y |
| -2 | 6 |
| 1 | 3 |
| 3 | 1 |
| 4 | 0 |
| 10 | -6 |
Slope:
y-intercept:
Equation:
12.
| x | y |
| 5 | 6.8 |
| 6 | 7 |
| 7 | 7.2 |
| 8 | 7.4 |
| 9 | 7.6 |
Slope:
y-intercept:
Equation:
Point-Slope Form: [latex]y-y_{1}=m(x-x_{1})[/latex]
Write an equation of the line in point-slope form through the given point and with the given slope m. Then graph the line on the coordinate plane. Clearly show 3 points on the line.
13. (-3, -5); [latex]m = -2[/latex]
Equation:

14. (0, -3); [latex]m=-\frac{1}{2}[/latex]
Equation:

Identify the slope and the point
15. [latex]y-2=2(x+3)[/latex]
Slope:
Point:

16. [latex]y+5=-\frac{3}{4}(x-4)74[/latex]
Slope:
Point:

Write an equation in point-slope form for the line.
17.
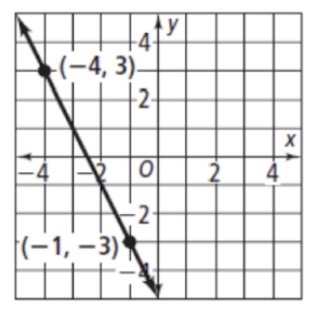
Write an equation in point-slope form of the line through the given points. Then write the equation in slope-intercept form. (Slope-intercept: [latex]y=mx+b[/latex])
18. (0, 4), (1, 7)
Slope:
Point-slope:
Slope-intercept:
19. (-2, -9), (3, 11)
Slope:
Point-slope:
Slope-intercept:
20. (2, 2), (5, -4)
Slope:
Point-slope:
Slope-intercept:
Standard Form [latex]Ax+By=C[/latex]
Graph each equation using the x– and y-intercepts. Show work for finding the intercepts.
21. [latex]-5x+y=-10[/latex]
x-int. [latex](\rule{5mm}{0.15mm},\rule{5mm}{0.15mm})[/latex]
y-int. [latex](\rule{5mm}{0.15mm},\rule{5mm}{0.15mm})[/latex]

22. [latex]-3x-6y=12[/latex]
x-int. [latex](\rule{5mm}{0.15mm},\rule{5mm}{0.15mm})[/latex]
y-int. [latex](\rule{5mm}{0.15mm},\rule{5mm}{0.15mm})[/latex]

For each equation, identify whether its graph is a horizontal or a vertical line, state the slope, then draw a graph. Graph all four lines on the same coordinate plane. Label each line with its equation.
 23. [latex]y=-5[/latex]
23. [latex]y=-5[/latex]
horizontal/vertical
Slope:
24. [latex]x=-4[/latex]
horizontal/vertical
Slope:
25. [latex]x=7[/latex]
horizontal/vertical
Slope:
26. [latex]y=8[/latex]
horizontal/vertical
Slope:
Write each equation in standard form using integers.
27. [latex]y-4=5(x-8)[/latex]
28. [latex]y=x-4[/latex]
29. [latex]y=\frac{-3}{5}x+2[/latex]
Write an equation that passes through the pair of points in point-slope form, slope-intercept form, and standard form using integers.
30. (4, -2), (5, -4)
Slope:
Point-slope:
Slope-intercept:
Standard:
31. (-5, -5), (10, 4)
Slope:
Point-slope:
Slope-intercept:
Standard:

