1.1 Exercises

1) Below is a (white) rectangle with length 5 units and width 3 units surrounded by a shaded border. How many shaded border tiles are there?

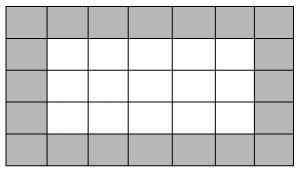
2) Consider a rectangle with length 10 units and width 4 units surrounded by a shaded border of unit squares like the border in #1. Draw a corresponding picture below and state how many border squares there are .

3) Consider a rectangle with length 100 units and width 37 units surrounded by a shaded border. Draw a corresponding picture and state how many border squares there are. Try to think of a way to do this without having to draw and count every square one by one.  Clearly describe how you figured out the number of shaded border squares .

4) Find an algebraic expression that represents the number of squares needed to build a border around a rectangular grid with length L units and width W units.

Draw a picture that represents your thinking and explain how you figured this out .

5) Think of a different way (than in #4) to figure out the number of squares needed to build a border around a rectangular grid with length L units and width W units. Write a corresponding algebraic expression and draw a picture. This should look different than your expression for #4 but should be equivalent to it .

6) Show that your algebraic expressions for part #4 and #5 are equivalent using algebraic operations on one or both expressions.