What is Algebra?

According to one source at

https://wagner.nyu.edu/files/students/Math_Review_-_Algebra_Operations.pdf

Algebra is a branch of mathematics that uses mathematical statements to describe relationships between things that vary. 

For example, we could use a mathematical statement to describe the relationship between the width of a cube (length=width=height) and its surface area.

When we use a mathematical statement to describe a relationship, we often use letters (that are called “variables”) to represent the quantities that vary, since the values of these quantities change (depending on the width of the cube).

1.1 Examples

Example 1.1.1

Determine the surface area for a cube with width 7 cm in two ways as follows.

Way 1: Using algebra (creating an equation that relates the width, w, to the surface area, S, and then using your equation find the answer). Be sure to define your variables clearly here .

Way 2 (to determine the surface area for a cube with width 7 cm):  Using objects (handout cubes) arithmetic and pictures (as if you are presenting to a class that does not know algebra).  Explain your process and show your work below .

Example 1.1.2

Below is a large square made up of 100 smaller unit squares (1 by 1). The unit squares along the border are shaded.

Without counting one by one, try to figure out how many shaded border squares there are in the picture.  State your answer below and clearly describe how you found it. It might help to mark up the figure above to illustrate your approach.  Then check your answer by counting the squares one by one.

Share your approach with other students in the class and if you come across a different approach, describe it below.

Taban calculated the number of border squares as (10 x 4) – 4. He justifies his answer as follows:

Since the dimensions of the big square are 10 x 10, there are 10 squares along each of the four sides. So that gives me 40 shaded border squares. But then each corner is part of two different sides. I’ve counted each of the corners twice. So I need to make up for that by subtracting 4 at the end.

Taban showed the picture below to illustrate his explanation:

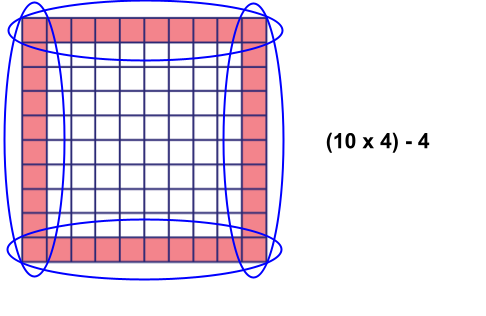
• What do you think of Taban’s solution? Are you convinced? Could he have explained it more clearly?

• How did Taban’s solution compare/contrast with your own?

• Explain how Taban’s shading and circling in his picture helps justify his answer.

Below are expressions that other students used to calculate the number of shaded squares along the border of a 10 x 10 square.  For each expression, write a justification that explains why that expression represents the number of shaded border squares correctly. Do NOT modify the expression, as it represents the student’s approach that you are trying to explain.  It might be helpful to include a sketch of the square and illustrate your reasoning.

1. Valentino calculated 10 + 10 + 8 + 8

2. Kayla calculated 4 x 9

3. Lin calculated (10 x 10) – (8 x 8 )

4. Marco calculated (4 x 8) + 4

5. Denzel calculated 10 + 9 + 9 + 8

Example 1.1.3

Consider the 6 by 6 square below.  Shade the border squares and use one of the techniques from example 1.1.2 to calculate the number of shaded border squares. Write an explanation and mark the picture below to illustrate your reasoning.

Example 1.1.4

Consider the 25 by 25 square with shaded unit squares along the border as shown below.  Use one of the techniques from example 1.1.2 to calculate the number of shaded border squares.  Write an explanation and mark the picture below to illustrate your reasoning.

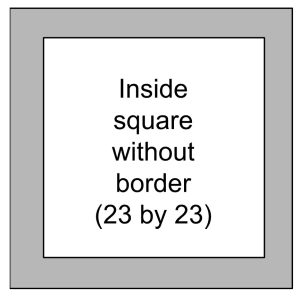
Example 1.1.5

If you have an n by n square with shaded border squares, how many (unit) shaded border squares will there be? Justify your answer with words and a picture.

1. Suppose you have 64 unit squares. Can you use all of these to make the border of a square? If yes, what are the dimensions of the square with the border? If no, why not? Explain your reasoning below.

2. Answer the same question in part (a) for 30 unit squares and explain your reasoning.

3. Answer the same question in part (a) for 256 unit squares and explain your reasoning.

4. If you have k shaded unit squares, explain how you can determine whether or not you may use all of these shaded squares to make the border of a larger square. If so, what would be the dimensions of the entire square (with border included)?
   Explain your reasoning and sketch a corresponding picture below.