1.4 The Use of Variables in Algebra
Pre-Class Work
Go to Visualizing Algebraic Equations Using a Balance Beam (Open in new window)
- Use the sliders to balance the scale according to the given equation
- Click on “solve” in the lower right corner and use the slider that appears to view the steps. Review the steps carefully (more than once if needed) to make sure you understand the connection between the scale and the algebra.
- Click on “new problem” and repeat the process.
- Go through at least 3 problems like this.
- Draw a scale picture that represents the equation 4x + 5 = 21. Solve this equation algebraically and for each step, draw a corresponding scale picture that represents the equality. Be prepared to share in class.
Illustration
The figure below shows bags containing bags and single blocks on a scale. The bags are marked with a “?” because they contain some unknown number of blocks. Each bag contains the same number of blocks and the scale is balanced.
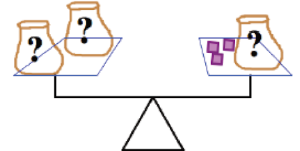
In order to determine how many blocks are in each bag we can take one bag from each side of the scale and see that one bag weighs the same as 3 blocks and hence each bag contains 3 blocks.
Alternatively, we may use a variable in an equation as follows:
Let x = the number of blocks in each bag.
Create an equation involving x based on the fact that the scale is balanced.
[latex]2x = x + 3[/latex]
Solve for x.
[latex]2x = x + 3[/latex] (subtract x from both sides)
[latex]x = 3[/latex]
Notice how subtracting x from both sides corresponds to removing one bag from each side of the scale.
Examples
Example 1.4.1
For parts (a) and (b), determine the number of blocks in each bag.
Explain your answer in two ways:
(1) without using a variable or equation
(2) by forming an equation with a variable and solving it.
a)
(1) without using a variable or equation
(2) by forming an equation with a variable and solving it.
b)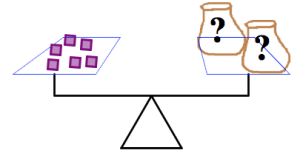
(1) without using a variable or equation
(2) by forming an equation with a variable and solving it.
Example 1.4.2
Draw a scale figure similar to those in Example 1.4.1, that represents the equation 5x + 2 = 3x + 8 where x is the number of blocks in each bag. Then, solve the equation. For each step, draw a corresponding scale picture and explain what scale action was taken to get from the previous step to the current step.
Example 1.4.3
Draw a (bag/block) scale figure that represents each of the following equations and state what the variable represents. Then, solve the equation. Explain the implications of your results in terms of the scale figure, as if you were talking to an elementary school student.
a) [latex]4p + 7 = 4p + 7 [/latex]
b) [latex]3y + 7 = 3y + 2[/latex]
Example 1.4.4
Create a (bag/block) scale figure problem where the answer is not a whole number. Draw a corresponding picture below. Solve it and explain your answer in terms of bags and blocks.
Different Types of Variables
The type of variable that we are dealing with depends on how it is used (in an equation).
| Type of variable | Illustration |
| Variable as a single unknown quantity (that we can find) | In the equation [latex]2y = 3 - 4y[/latex]
y is a variable that is a single unknown that we can solve for and get a single value |
| Variables as quantities that relate to each other (in an equation with two or more variables) | In the equation [latex]L\times W=24[/latex]
L and W are related to each other in a way that the value of one determines/depends on the value of the other. |
| Variables that can be any number (in an equation that is always true, as in a rule or property) | In the equation [latex]a(b+c)=ab+ac[/latex]
a, b and c may be any number since the equation is always true (distributive property) |
Variable type is not to be confused with what a variable represents in a given scenario. For example in the equation [latex]L\times W=24[/latex], L and W are quantities that relate, referring to the type of variable they are as described in the table above.
But when describing what each variable represents in the scenario of rectangle area equaling 24, L represents the length of the rectangle and W represents the width of the rectangle.
Example 1.4.5
Let h represent the number of hours and d represent the number of days.
a) Which of the following equations correctly shows a relationship between the two variables? Explain your answer and give an example using specific numbers.
[latex]h = 24d[/latex] or [latex]d = 24h [/latex]
b) What types of variables are h and d, based on the table above?
Illustration
a) Consider the following scenario: Drena has double $300 more than Jasper and together they have $900.
This scenario may be represented by the following equation: [latex]2(x + 300) + x = 900[/latex].
Variable type of x: single unknown
What does x represent? The amount of money that Jasper has
b) Assume the equation [latex]25x = 2y[/latex] represents that there are two teachers for each class of 25 students.
Variable type of x and y: quantities that relate
What do x and y represent? x represents the number of teachers and y represents the number of students.
c) Consider the following equation: [latex](a\times b)^{x}=a^{x}\times b^{x}[/latex]
Variable type of a, b and x: Any number
What do a, b and x represent? Any number
The only situation in which we get the same answer for variable type and what the variable represents is when we have an equation that is always true no matter what values we plug in for them as in part (c) of the illustration above.
Example 1.4.6
For each of the following scenarios and corresponding equations, state what each variable represents in terms of the given situation and state what type of variable it is, based on the table above (single unknown, quantities that relate, any number).
a) Jazz has 12 coins in dimes and quarters, for a total of $1.95 (one dollar and 95 cents) in change: [latex]25x + 10(12 - x) = 195[/latex].
Variable type of x:
What does x represent?
b) The square root of a product is the product of the square roots: [latex]\sqrt{a \times b}=\sqrt{a} \times \sqrt{b}[/latex]
Variable type of a and b:
What do a and b represent?
c) To make an apple pie you need 3 cups of sugar for every 10 apples: [latex]y=\frac{10}{3}x[/latex]. This one is a bit tricky so it might be helpful to plug in some numbers.
Variable type of x and y:
What do x and y represent?
Example 1.4.7
Consider the following scenario. Three chickens weigh the same as a monkey. Two monkeys and a chicken weigh the same as a sheep. Let 𝐶 represent the weight of one chicken, 𝑀 represent the weight of one monkey and 𝑆 represent the weight of one sheep.
a) Write two equations that represent the relationships in the problem.
b) Determine how many chickens weigh the same as one sheep.
c) What types of variables are C, M and S?
Example 1.4.8
Write word problems that would be appropriate for each of the following equations. Try to incorporate some cultural diversity into your scenarios that might resonate with a diverse student population.
a) [latex]x - 11 = 45[/latex]
b) [latex]3x = 42[/latex]
c) [latex]3x + 12 = 4x + 10[/latex]
a statement (with an equal sign) asserting that two expressions have the same numerical value
a letter that represents a quantity that may vary

