2.2 Exercises
1) Answer each question below for the following pattern. Show and/or explain how you got your answers. Assume each tile is 1cm by 1cm.

a) Write a recursive formula for the number of tiles in the nth figure.
b) Write an explicit formula for the number of tiles in the nth figure.
c) Write a recursive formula for the perimeter of the nth figure.
d) Write an explicit formula for the perimeter of the nth figure.
2) Answer each question below for the following pattern. Show and/or explain how you got your answers. Assume each tile is 1cm by 1cm.
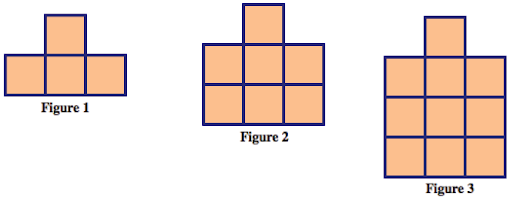
a) Write a recursive formula for the number of tiles in the nth figure.
b) Write an explicit formula for the number of tiles in the nth figure.
c) Write a recursive formula for the perimeter of the nth figure.
d) Write an explicit formula for the perimeter of the nth figure.
3) Consider the pattern shown below. Observe that the square grid that is 3 units long is made from 24 unit-long segments.
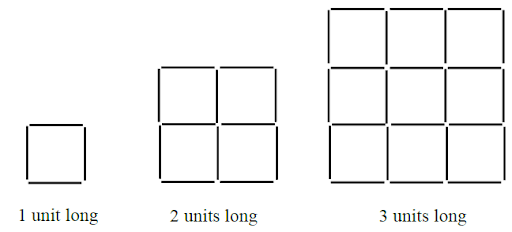
a) How many segments are required to make a square grid that is 10 units long?
b) Write a recursive formula for the number of segments required to make a square grid that is n units long. Show and/or explain how you got your answer.
c) Write an explicit formula for the number of segments required to make a square grid that is n units long. Show and/or explain how you got your answer.
For more practice with growing patterns go to https://www.visualpatterns.org/ and try to find recursive and explicit formulas for some of the patterns.
A recursive formula for a sequence identifies initial term(s)/number(s) in the sequence and then gives a rule for finding each subsequent term in the sequence using one or more previous terms.
A formula for the nth term of a sequence in which we may plug in the value of n to determine the nth term without using previous terms.

