2.2 Growing Patterns
Pre-Class Work
Go to https://www.geogebra.org/m/snwkdwxj (opens in a new tab)
1) For the first problem, follow the instructions in building the 4th figure and check it. Sketch the first 4 figures below.
2) Enter an equation as prompted, record your equation below and state exactly what each variable represents.
3) Explain how you determined your equation, even if it is not correct.
4) If your equation is not correct, keep trying until you either get it correct or you are given a “Possible Solution”. Record the result (your correct solution or the “possible solution”) below and explain why it is correct.
5) Try another problem by clicking on “New Problem”
In this section we look at different types of patterns known as growing patterns where each subsequent figure grows in a distinct way. We start with patterns of growing tile figures.
2.2 Examples
Example 2.2.1
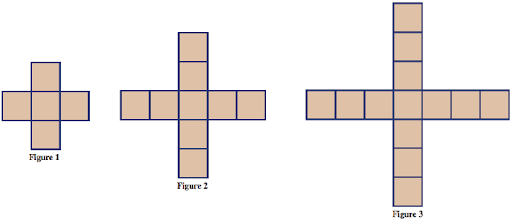
a) Describe in words how you see the pattern growing. Focus on what stays the same and what changes from one figure to the next.
b) Calculate the number of tiles you would need to build each figure up to figure 10 and record your answers in the table below.
| Figure | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| # of tiles |
c) Calculate the number of tiles you would need to build the 100th figure in the pattern.
d) Describe how you can figure out the number of tiles in any figure in the pattern. In particular, come up with a formula for the number of tiles in the nth figure. Justify your answer based on how the pattern grows.
e) Could you make one of the figures in the pattern using exactly 25 tiles? If yes, which figure? If no, why not? Justify your answer.
f) Could you make one of the figures in the pattern using exactly 100 tiles? If yes, which figure? If no, why not? Justify your answer.
Example 2.2.2

a) Describe in words how you see the pattern growing. Focus on what stays the same and what changes from one figure to the next.
b) Calculate the number of tiles you would need to build each figure up to figure 10 and record your answers in the table below.
| Figure | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| # of tiles |
c) Calculate the number of tiles you would need to build the 100th figure in the pattern.
d) Describe how you can figure out the number of tiles in any figure in the pattern. In particular, come up with a formula for the number of tiles in the nth figure. Justify your answer based on how the pattern grows.
e) Could you make one of the figures in the pattern using exactly 25 tiles? If yes, which figure? If no, why not? Justify your answer.
f) Could you make one of the figures in the pattern using exactly 100 tiles? If yes, which figure? If no, why not? Justify your answer.
Example 2.2.3
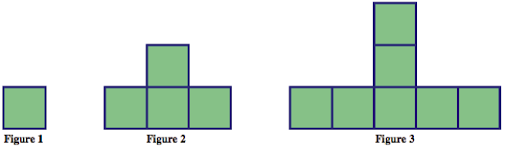
a) Describe in words how you see the pattern growing.Focus on what stays the same and what changes from one figure to the next.
b) Calculate the number of tiles you would need to build each figure up to figure 10 and record your answers in the table below.
| Figure | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| # of tiles |
c) Calculate the number of tiles you would need to build the 100th figure in the pattern.
d) Describe how you can figure out the number of tiles in any figure in the pattern. In particular, come up with a formula for the number of tiles in the nth figure. Justify your answer based on how the pattern grows.
e) Could you make one of the figures in the pattern using exactly 25 tiles? If yes, which figure? If no, why not? Justify your answer.
f) Could you make one of the figures in the pattern using exactly 100 tiles? If yes, which figure? If no, why not? Justify your answer.
Discussion
There are two main ways to describe growing patterns as follows:
Way 1: Using a recursive formula which determines the number for the next figure using the number for the previous figure. Recursive formulas have two components:
- The number for the first figure (first figure number = ?)
- A rule that describes the number for the nth figure by adding something to the number for the previous figure (nth figure number = ? in terms of figure (n-1) number)
Way 2: Using an explicit formula which gives a rule for the nth figure without using previous figures (only uses the figure number n). For explicit formulas we determine a rule for the pattern and express it as a general formula for the desired number in figure n.
For Example 2.2.1 (copied below), check the recursive and explicit formulas for several n values. Then click on the arrow to complete the recursive formulas for Examples 2.2.2 and 2.2.3 by filling in the blanks.
Think – Pair – Share
Think about how the recursive and explicit formulas for each pattern above are related.
Pair up with someone in the class to share each other’s thoughts on the matter.
Describe in general, how the recursive and explicit formulas are related so that your explanation could be used for any of the three examples. Then check your reasoning with each example. Record your explanation and work below.
Example 2.2.4
Assume each tile in the patterns from examples 2.2.1 through 2.2.3 is a 1 cm by 1 cm square. Determine recursive and explicit formulas for the perimeter of the nth figure in each pattern. Explain how you arrived at your answers.

Recursive Formula for perimeter:
Explicit Formula for perimeter:

Recursive Formula for perimeter:
Explicit Formula for perimeter:

Recursive Formula for perimeter:
Explicit Formula for perimeter:
Example 2.2.5
A common way of constructing bridge trusses (frames made from triangles) is shown below. Observe the truss that is 1 unit long is constructed from 3 unit-long beams, the truss that is 2 units long is constructed from 7 unit-long beams and the truss that is 3 units long is constructed from 11 unit-long beams.
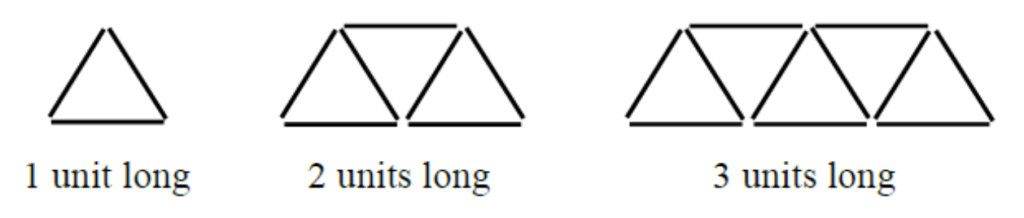
a) Finishing filling in the table below
| Truss length | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| # of unit beams needed | 3 | 7 | 11 |
b) How many beams are required to make a truss that is 50 units long? Explain how you got your answer.
c) Write a recursive formula for the number of beams needed to make a truss n units long. Explain how you got your answer.
d) Write an explicit formula for the number of beams needed to make a truss that is n units long. Explain how you got your answer.
e) Share your formula and explanation with a classmate. If your formulas and explanations are the same, write another explicit formula for the number of beams required to make a truss n units long, counting the beams in a different way. Explain how you got your answer. Then prove the two expressions are equivalent using algebraic operations.
Example 2.2.6
Consider the growing pattern below. Answer the questions that follow. Explain and/or show how you got your answers.
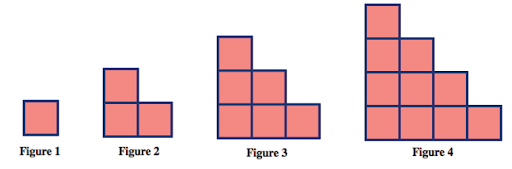
a) Write a recursive formula for the number of tiles in figure n.
b) Write an explicit formula for the number of tiles in figure n. This will require some creative thinking. Drawing pictures should help as well. Don’t be afraid of trial and error and check your conjectures. There is a pictorial hint at the end of this chapter (that shows one way to think about it) but try to get it on your own before looking. Also note that there is more than one way to determine this formula.
A recursive formula for a sequence identifies initial term(s)/number(s) in the sequence and then gives a rule for finding each subsequent term in the sequence using one or more previous terms.
A formula for the nth term of a sequence in which we may plug in the value of n to determine the nth term without using previous terms.

