3.2 Exercises

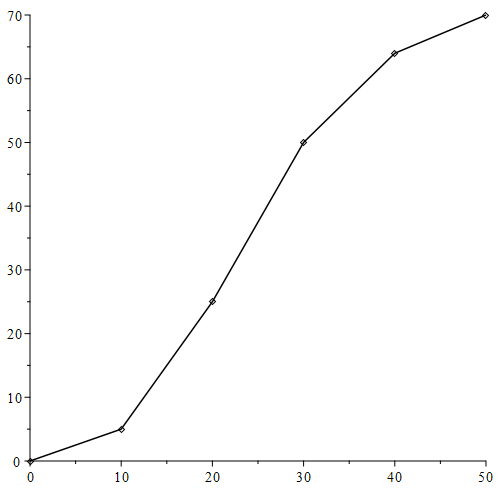
1) Reconsider the push up data copied below.

Time in seconds (input t) 0 10 20 30 40 50
Total number of push ups (output P) 0 5 25 50 64 70

a. What is the average rate of change of the total number of push-ups from 20 to 40 seconds?

 

 

 

 

b. What does the answer to part (a) tell us about the number of push-ups?

 

 

 

 

 

c. Show (and explain) on the graph below what your answer to (a) means in terms of slope.
Graph of the following points from the given table with each adjacent pair of points connected by a straight line segment: (0,0), (10,5), (20,25), (30,50), (40,64), (50,70) In particular the following pairs of points are connected by line segments: (0,0) and (10,5) (10,5) and (20,25) (20,25) and (30,50) (30,50) and (40,64) (40,64) and (50,70)

 

 

2) Consider the graph below representing the number of customers served at a Chick-fil-A as a function of time in hours.

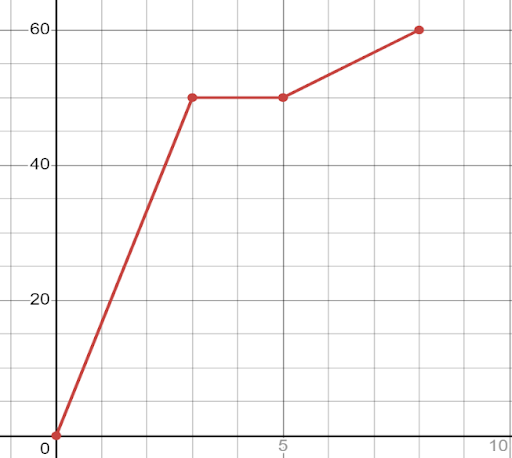
Graph with minutes on the horizontal axis and miles per hour on the vertical axis. Points at (0,0), (1,30), (2,30), (4,0), (4.5,0), (5,30), (6,30), (6,60), (10,60), (12,0) with adjacent points connected by a straight line. In particular the following points are connected by line segments: (0,0) and (1,30) (1,30) and (2,30) (2,30) and (4,0) (4,0) and (4.5,0) (4.5,0) and (5,30) (5,30) and (6,30) (6,30) and (6,60) (6,60) and (10,60) (10,60) and (12,0)

 

a. Find the average rate of change from 0 to 3 and explain what information this gives you about the customers.

 

 

 

 

 

 

 

 

b. Find the average rate of change from 0 to 7.5 and explain what information this gives you about the customers.

 

 

 

 

 

 

 

 

c. What do you think the horizontal line segment signifies?

 

 

 

3)  The height H, of an object dropped from the roof of an eight story building is given by the following equation [latex]H=-16t^{2}+64[/latex] where H is the height of the object in feet, t seconds after it is dropped. Find the average rate of change of H from 0 to 2 seconds and explain what it tells us about the height of the object.

 

 

 

 

 

 

 

 

 

4) The temperature F in degrees Fahrenheit t hours after 6 AM is given by the following equation [latex]F(t)=-\frac{1}{2}t^{2}+8t+32[/latex].

 

a. Find the average rate of change of F from [latex]t = 4[/latex] to [latex]t = 8[/latex] and explain what it tells us about the temperature.

 

 

 

 

 

 

 

 

 

 

b. Find the average rate of change of F from [latex]t = 8[/latex] to [latex]t = 12[/latex] and explain what it tells us about the temperature.

 

 

 

 

 

 

 

 

 

 

c. Find the average rate of change of the temperature between 10 AM and 6 PM.

 

 

 

 

 

 

definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Algebra, Patterns, and Functions for Elementary School Teachers: A Workbook Approach Copyright © 2024 by Mary Ann Barbato is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book