Pre-class Work

1) Watch the following videos on the distributive property. Find something about the use of symbols in the second video that may be confusing to viewers. Explain below.

Distributive property in arithmetic:

Distributive property in algebra:

2) Watch this video demonstrating how area may be used to multiply two digit and three digit numbers.

3) Watch the following video on the FOIL method: The FOIL Method. Find a point in the video where the person talking uses the wrong terminology/word.  Explain below.

4) Read and work through checkpoint exercises at Section A.8: Factoring Quadratic Trinomials as needed for review on factoring. Be prepared to ask questions in class.

The association between arithmetic and geometry is ancient. A number can be thought of as a length, and addition can be thought of as combining lengths.

Areas of rectangles can be found by multiplying the side lengths. Of special interest are squares (rectangles with equal side lengths). The area of a square can be found by multiplying those equal side lengths together. And that is why  is commonly referred to as “ squared”, originally meaning “take the length of  and make a square with that side length and take its area”. Equations involving only constant, , and  terms are called quadratic equations. The word quadratic refers to the square (“quad” is Latin for “four”, for the four-sided square).

In this section we focus on a geometric way of looking at quadratic expressions.  We illustrate the product of two binomials or a monomial (one term) and a binomial (two terms) with area, using a technique similar to that shown in pre-class work #2 video.

In particular, our goal will be to build rectangles whose area represents these products.  This will enable us (and our future students) to see why the FOIL method works and how the distributive property plays an important role.

To do this we will use three different types of rectangles shown below:

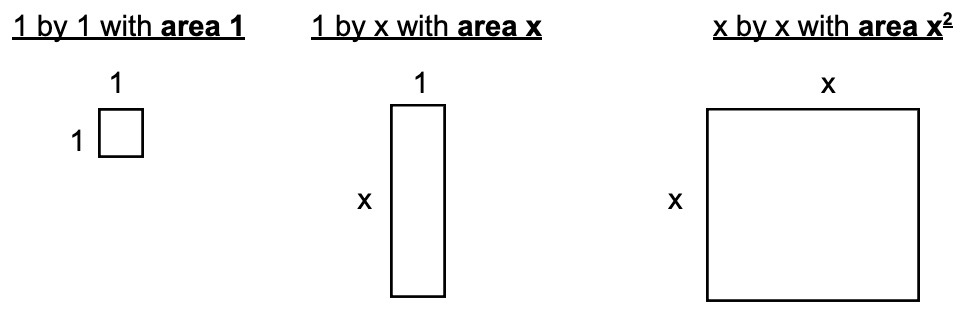
(Handout algebra tiles, if available)

Assume each corresponding algebra tile has the areas given above.

5.1 Examples

Example 5.1.1

Use your algebra tiles to form a rectangle with length [latex](x + 3)[/latex] and width [latex](x + 2)[/latex] as shown below. Label each tile with its area.  Then add all the areas together and state your answer below.

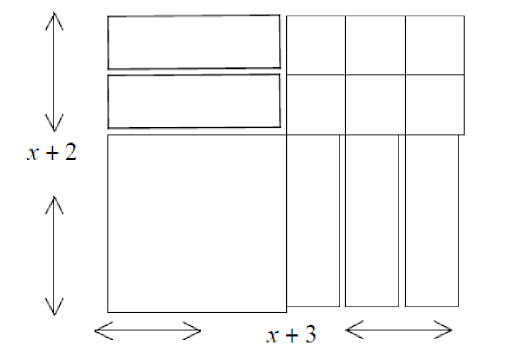
Your total area should be equal to the length times the width, that is [latex](x+2)(x+3)[/latex].

Now use the FOIL method to confirm your answer.  Show your work below.

How is the FOIL method related to the distributive property?  Looking at the example above, we can view it as follows:

Distribute [latex](x+3)[/latex] to x and 2:  [latex](x+2)(x+3) = x(x+3) + 2(x+3)[/latex]

Distribute x into [latex](x+3)[/latex] and 2 into [latex](x+3)[/latex]: [latex]x^{2} + 3x + 2x + 6 [/latex]

Add like terms: [latex]x^{2} + 5x + 6[/latex]

So, FOIL is really applying the distributive property twice.

Now you try.

Multiply [latex](x+2)(x+3)[/latex] in a similar way by first distributing the [latex](x + 2)[/latex] to x and 3.  Show work below.

How does the algebra tile method relate to the distributive property?  Discuss with a partner.  Use Example 5.1.1 to explain and make notes below.

When multiplying binomials with a negative term, we can use shading as shown in Example 5.1.2 to distinguish area representing a negative product.

Example 5.1.2

Consider the algebra tile representation of the product (x+2)(x-3) below.  Observe that the shaded tiles correspond to multiplying a positive term by a negative term resulting in a negative product. Label each tile with its area and put a negative sign in front of areas corresponding to a shaded tile.  Add all the areas together and state your answer below.

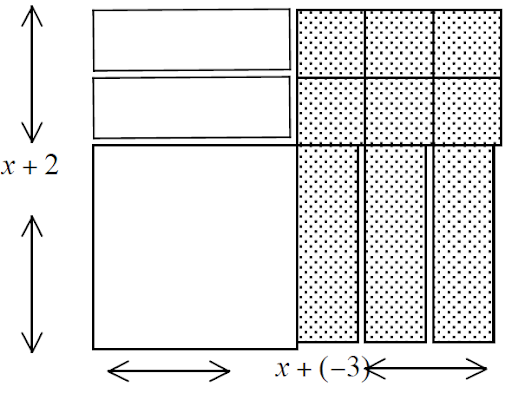
Now use the FOIL method to confirm your answer.  Show your work below.

Example 5.1.3

Sketch algebra tile rectangles for each of the following products.  Use algebra tiles as needed to help.  Be sure to label the dimensions of your rectangles as we did in previous examples.  Then, show the sum of the rectangle areas in expanded form before simplifying to get the final answer.  Work with a partner – each pair will be assigned one part below to work on and share with class.  If you finish your part early, try another part.

a) [latex](x+3)(x+4)[/latex]

b) [latex](-2x)(x+4)[/latex]

c) [latex](x+5)(x-2)[/latex]

d) [latex](x-2)(x-1)[/latex]

e) [latex](2x+3)(x-1)[/latex]

f) [latex](3x-2)^{2}[/latex]

Now let us use tiles and rectangle areas to factor.

Watch the following video that explains how the process works:

Example 5.1.4

Consider the quadratic expression [latex]x^{2}+6x+8[/latex]. Observe that this expression may be represented as the collection of tiles below

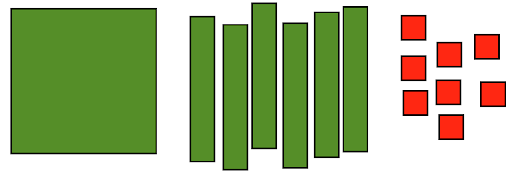
Use these algebra tiles to try to build a rectangle.  Sketch your rectangle below and label the side lengths.  The side lengths of your rectangle will be the factors of [latex]x^{2}+6x+8[/latex].

Example 5.1.5

Consider the quadratic expression [latex]2x^{2}-3x+1[/latex].  Use corresponding algebra tiles to build a rectangle and sketch your rectangle below. Make sure when you make your sketch you shade in the appropriate part to distinguish the negative term [latex]-3x[/latex].  Use your rectangle to factor [latex]2x^{2}-3x+1[/latex].

Example 5.1.6

Use algebra tiles to factor the following expressions as we did in previous examples.  Sketch your rectangles below, label the side lengths, and state the corresponding factors of the quadratic.   Work with a partner – each pair will be assigned one part below to work on and share with class.  If you finish your part early, try another part.

a) [latex]x^{2}+10x+25[/latex]

b) [latex]2x^{2}+7x+6[/latex]

c) [latex]2x^{2}+5x-3[/latex]

d) [latex]4x^{2}+9x+2[/latex]

e) [latex]6x^{2}+13x+5[/latex]