5.2 Exercises
1) Consider all rectangles with perimeter 24. Proceed as we did in Example 5.2.4 and develop a functional relationship between the base x and the area y as follows.
a) Draw all possible rectangles with perimeter 24 with whole number dimensions.
b) Fill in the table below based on your results from part (a)
| Base (x) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Area (y) | 0 | 0 |
c) Sketch and connect the points from your table.
d) Write an equation that expresses the base x as a function of the area y.
e) What is the highest point on the graph and what does it tell us about rectangles with perimeter 24?
2) Find the equation of each of the following quadratic functions represented in the tables below using one of the methods we learned. Which method you use depends on the information you have (e.g. vertex, intercepts).
a)
| x | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|---|---|
| y | 2.5 | -1 | -3.5 | -5 | -5.5 | -5 | -3.5 | -1 | 2.5 |
b)
| x | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|
| y | 14 | 3 | -2 | -1 | 6 | 19 |
c)
| x | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|
| y | -1 | -4 | -5 | -4 | -1 | 4 |
3) Answer the following questions for the parabola
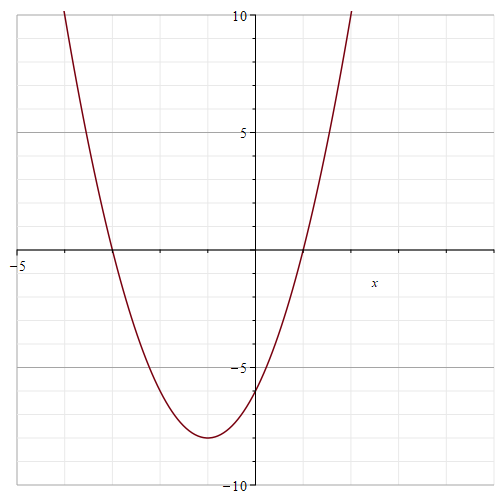
a) What are the x-intercepts? Mark them on the graph.
b) What is the line of symmetry? Sketch it with a dotted line on the graph.
c) What is the vertex? Mark it on the graph.
d) What is the equation for the function? Show your work.
4) Graph the following quadratic function. Be sure to find and show x and y intercepts and vertex for each.
a) [latex]y=x^{2}+4x-3[/latex]
b) [latex]y=x^{2}+5x+4[/latex]
c) [latex]y=4x^{2}-16x[/latex]
5) Which of the following relationships are quadratic? Justify your answer.
a) The relationship between the radius of a circle and its area.
b) The relationship between the length of a square and its perimeter.
c) The relationship between the radius of a sphere and its volume.
d) One soccer team has n players and the other has (n - 1) Each player from one team shakes every player’s hand on the opposing team. Consider the relationship between n and the number of handshakes.
a statement (with an equal sign) asserting that two expressions have the same numerical value
A function that may be expressed in the form [latex]y=ax^{2}+bx+c[/latex] where a, b and c are constants and a is not equal to zero. The graph of a quadratic function is a parabola.
The vertex of a quadratic function is the lowest point on the corresponding graph if the parabola opens up and the highest point on the graph if the parabola opens down.
The graph of a quadratic equation which is a u-shaped curve that is symmetric about the axis of symmetry.
See https://www.math.net/parabola for a more precise definition.
The x-intercept of function is the point at which the graph of the function intersects the x-axis (where y = 0).
The axis or line of symmetry of a quadratic function is the vertical line that goes through the vertex of the corresponding parabola.

