Chapter 5: Quadratic Functions
Print Version Only Chapter 5 Quadratic Functions – Informal Math Modeling
In this chapter…
- 5.1 Quadratic Expressions and Area
- 5.2 Quadratic Functions and Models
We previously studied linear models and several applications. However, many real world relationships are not linear. In this chapter we look at quadratic functions which are a common type of function that is non-linear, that is, the slope/rate of change is NOT constant. Such functions are used to model many relationships as we will see.
Although quadratic functions are not formally studied in elementary school mathematics, students may explore patterns that involve quadratic relationships.
Check out the lesson below from Everyday Mathematics (University of Chicago School Mathematics Project, 1995) in which second graders build square arrays that represent numbers multiplied by themselves and then explore the numerical patterns.
Lesson from Everyday Mathematics
Work in a small group
Materials:
- Centimeter grid paper
- Centimeter cubes or pennies
- Tape
Directions:
- Each person chooses a different number from 2 to 10
- Build an array that shows your number multiplied by itself. Use pennies or centimeter cubes.
- Draw each array on centimeter grid paper. Write a number model under each array.
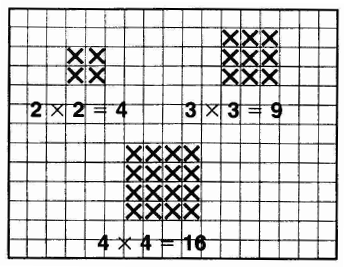
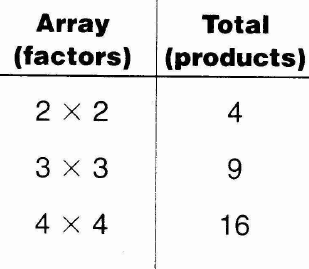
- Make and record and a few more arrays. On a blank sheet of paper, make a table like the one below. Begin with the smallest factors. Record them in order: 2 x 2, 3 x 3, 4 x 4 and so on.
- Continue working together. Build arrays with cubes or pennies for larger and larger numbers. Draw the arrays on grid paper. You may need to tape pieces of grid paper together for the larger arrays.
- Record the factors and products for the larger numbers in your table. Look for number patterns as studied in earlier chapters.
Such activities expose early elementary students to nonlinear relationships and also link to growing patterns as studied in earlier chapters.
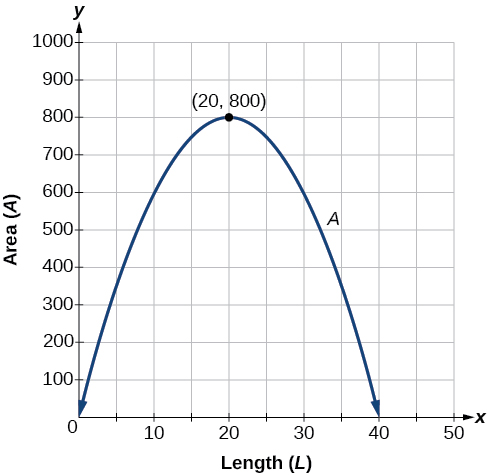
In middle school, students explore other quadratic relationships such as the relationship between the radius and the area of a circle or the relationship between the base of a rectangle and its area which we will explore later in this chapter.
As a reminder, it is important for elementary teachers to have an in-depth understanding of elementary AND middle school mathematics. In particular, the Massachusetts Department of Elementary and Secondary Education (DESE) requires that teacher candidates for K-6 have mastery of concepts in grade K – 8. See https://www.doe.mass.edu/edprep/domains/instruction/smk-guidelines.docx

