12.1, 12.2 Linear Equations and Scatter Plots

Problem 1

The following is a graph of a line:

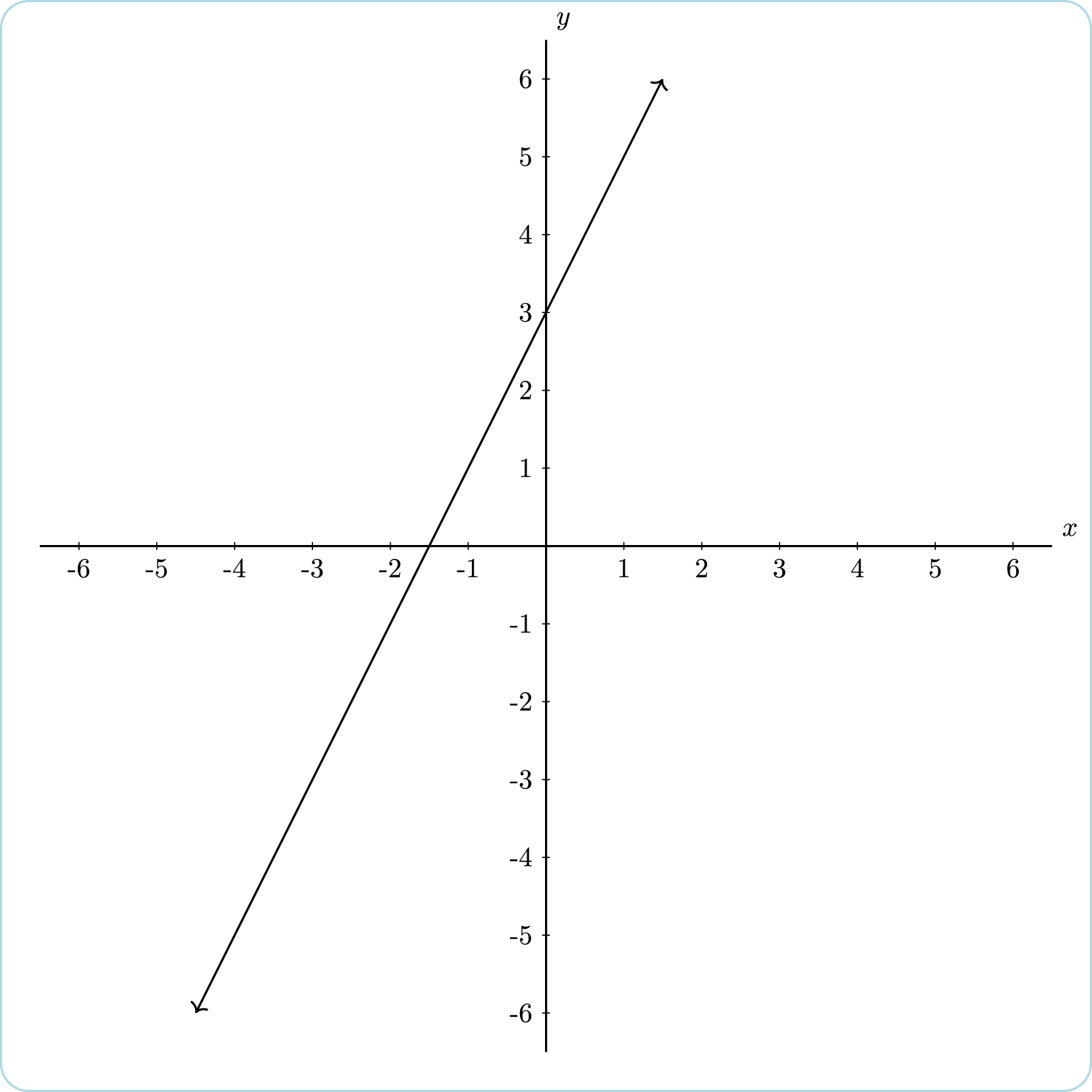
A line with a y-intercept of 3. Another point on the line is (1,).

Write the equation of the line [latex]y=[/latex]

 

Correct Answers

2x + 3

Problem 2

The following is a graph of a line:

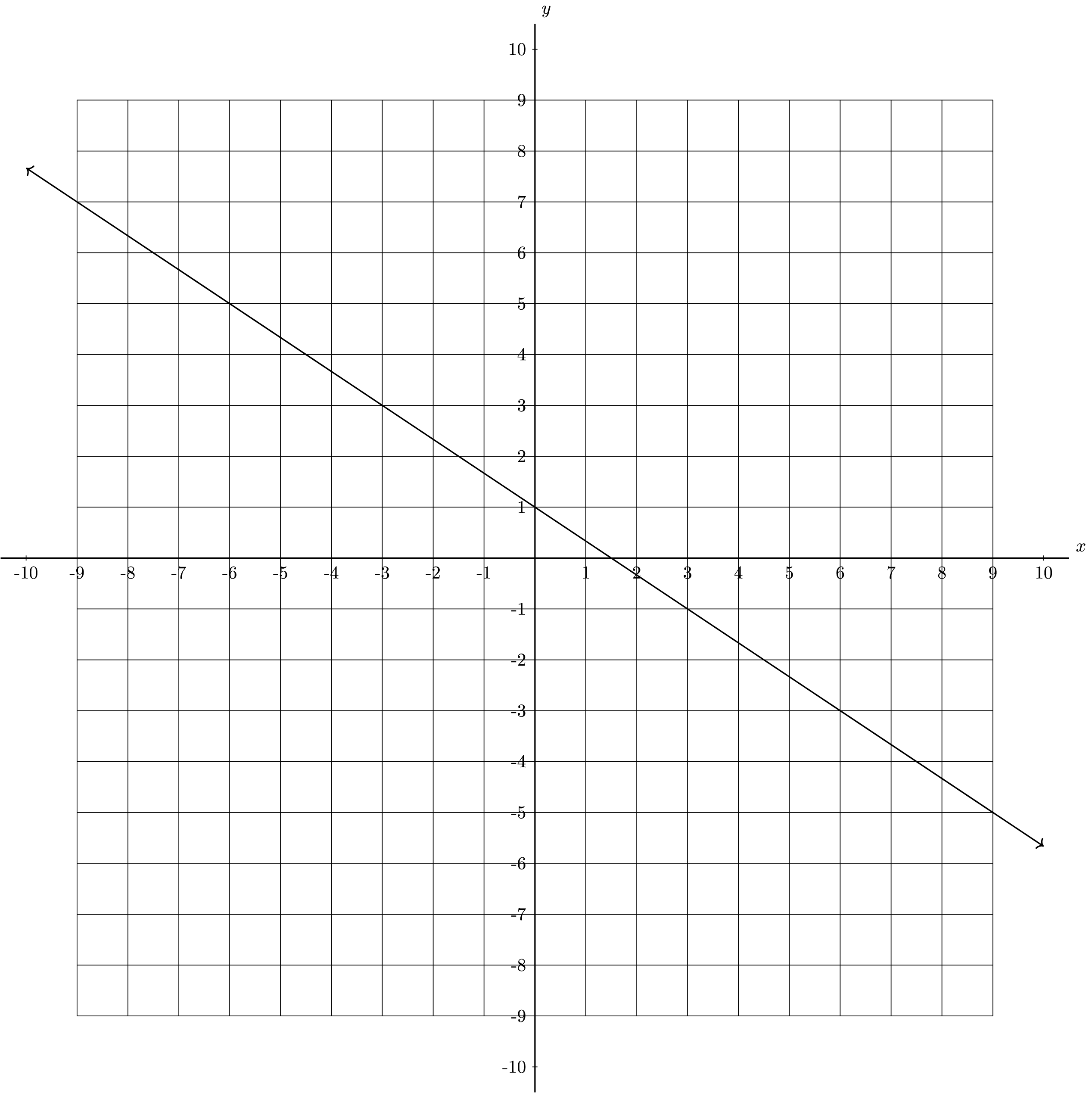
A line with a y-intercept of 1. Another point on the line is (9,-5).

Write the equation of the line [latex]y=[/latex]

Solution

A line’s slope-intercept equation has the form y = mx + b, where m is the slope and b is the y-intercept. We first find the slope.

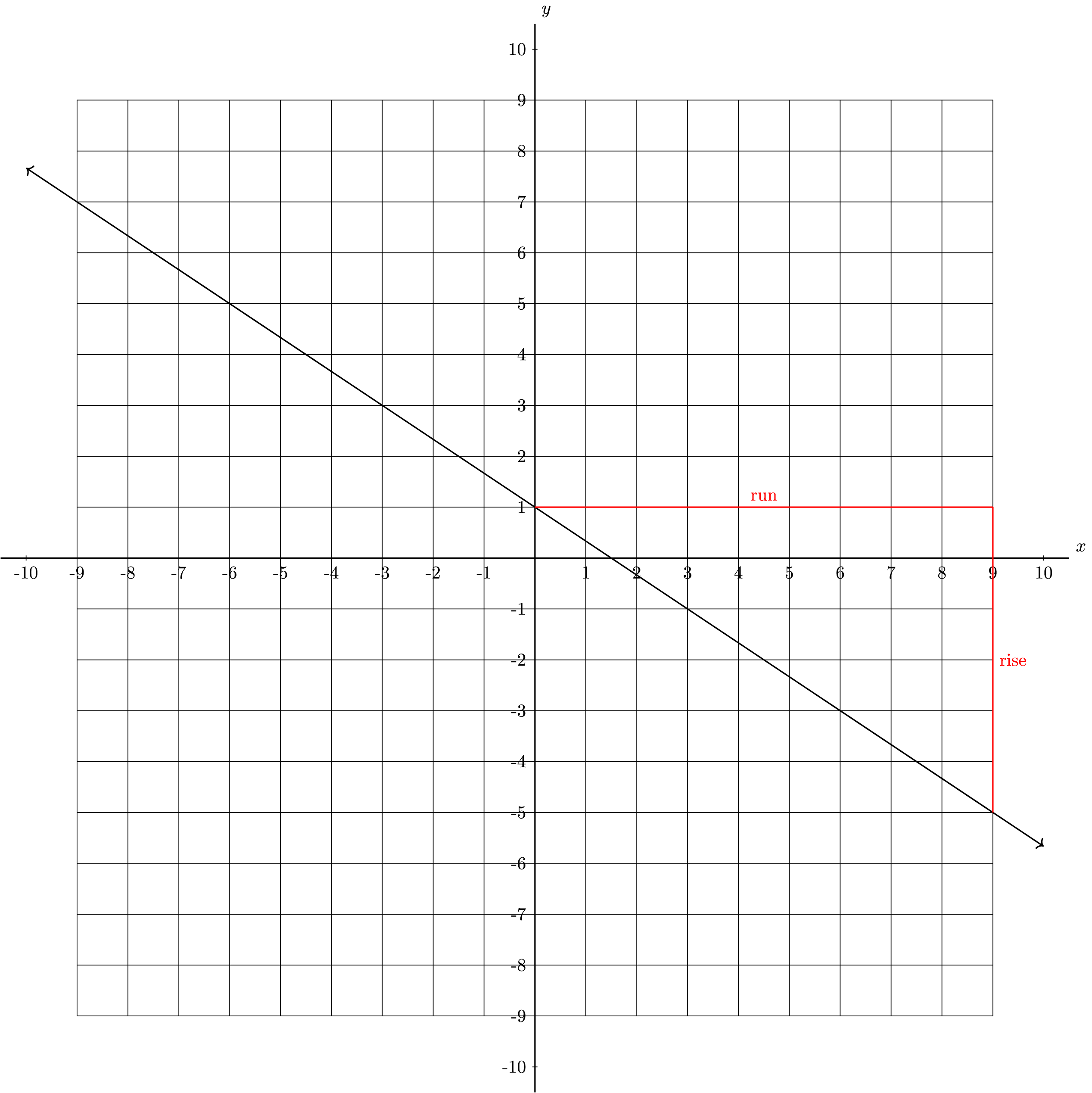
A line with a y-intercept of 1. Another point on the line is (9,-5). In addition, a horizontal line is drawn from (9,-5) to (9,1) and then a vertical line is drawn from (9,1) to (0,1)

To find the slope of a line from its graph, we identify two points, and then draw a slope triangle. It’s wise to choose points with integer coordinates. For this problem, we choose (0, 1) and (9, −5).

Next, we draw a slope triangle and find the “rise” and “run”. In this problem, the rise is −6 and the run is 9.

[latex]slope=\frac{rise}{run}[/latex]

[latex]=\frac{-6}{9}[/latex]

[latex]=-\frac{2}{3}[/latex]

This line’s slope is –[latex]\frac{2}{3}[/latex].

It’s clear in the graph that this line’s y-intercept is (0, 1).

So this line’s slope-intercept equation is [latex]y=-\frac{2}{3}x+1[/latex]

Correct Answers

-0.666667x+1

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Statistical Problem Sets in WeBWorK Copyright © 2023 by Rachael Norton and Peter Staab is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book